An update - Bcrypt and things
It’s been a little while since I’ve updated the devlog here; for the most part my activity for the last week or two has been focused on the proposal, and I’m just about done with an updated draft that accounts for all of the feedback - I’ll be posting that soon.
In the meantime, I still have been working on the bindings, and I have a lovely little update that I’ve been meaning to post for a few days.
The primary update is that I have:
- Fixed Botan.Low.Bcrypt INSUFFICIENT_BUFFER_SPACE exception
- Botan.Low.Bcrypt unit tests now pass
- Made improvements to
Botan.Bcrypt for easier use
- Fixed trailing NUL in bcrypt digests (may have been a regression)
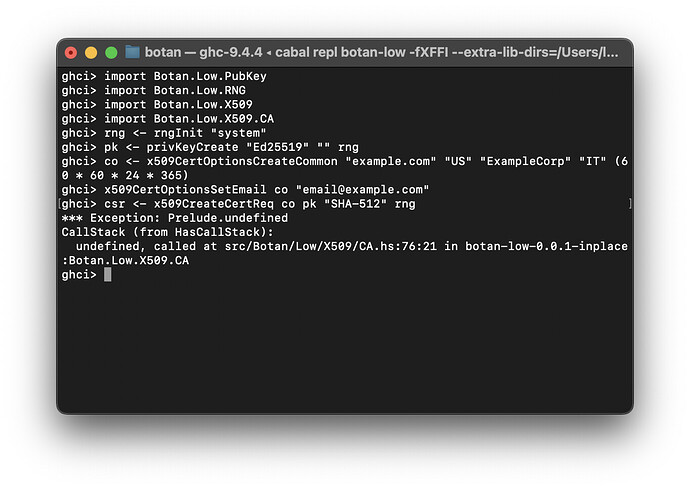
By going through the C++ source, I discovered that there was an unmentioned size pointer check that was being compiled out in most cases, except for tests. In some cases Botan uses size pointers to return the final length of the output, and sometimes it also uses the same pointer to take the output buffer length as an input. It turns out we need to poke the length of the output buffer here, as it was erroneously succeeding before because we were providing a buffer of adequate size but the check was being compiled out. 
Now Botan.Bcrypt should be good to go!
In addition to this, I did some work on public key exchange stuff because it is hanging indefinitely:
- Began work on
Botan.PubKey.KeyAgreement
- Discovered memory leak / hang in
Botan.Low.PubKey.KeyAgreement
- Function hangs until terminated by OS (Ctrl-C signal is blocked)
-
safe vs unsafe doesn’t seem to matter
- Occurs in
botan_pk_op_key_agreement function
- This is for DH, ECDH, Curve22519 key exchange, so high priority
- Checked some different versions of GHC to make sure its not a version-specific bug, need to test more thoroughly
- Will be going over C++ and Z-Botan source to figure it out
And now for something a little bit unusual - Merkle Trees!
I’ve been working on this project for a while, and I thought it would be good to show a bit of where this cryptography project is headed, long-term, while I finish updating the proposal pull request.
You see, I didn’t just idly decide to spend my time writing bindings to a cryptography library. I want to be able to express some very particular cryptography constructs, and I want to express them properly - and that means starting with a solid foundation. That foundation is now solid enough to begin building some of those constructs.
One of those constructs is Merkle, an abstraction of the core concept behind sparse merkle trees. A merkle tree is a data structure that hashes objects and combines their digests in order to provide integrity and cryptographic proofs for many pieces of data. Such structure form the basis of many distributed cryptosystems but often implementations are highly-concrete, focused on binary optimization rather than ease of understanding, and take pages upon pages to explain and justify everything. That never sat well with me.
Today, I’m here to show you how to build a sparse merkle tree with just a few lines of code, and we will do it in a way that barely mentions cryptography, and allows us to define arbitrary merkle data structures in an incredibly concise manner.
Are you ready to speedrun some merkle trees? We start with our ideal hash class from earlier:
data family Digest a
class Hash a where
hash :: ByteString -> Digest a
digest :: Digest a -> ByteString
A sparse merkle set / map is intimately related to a unital magma algebra, or what you might call a non-associative, non-commutative monoid. As such, we can define it by extending the Hash typeclass to Merkle by adding an empty and append function.
class (Hash a) => Merkle a where
merkleHash :: ByteString -> Digest a
merkleEmpty :: Digest a
merkleAppend :: Digest a -> Digest a -> Digest a
One advantage of this approach is that its conceptual reliance on cryptography is low, an implementation detail. This becomes important in the future when I start blending this with indexed recursion schemes because there are more tight mathematical connections there (but we won’t get to that today  we’re getting close).
we’re getting close).
Conceptually, merkleEmpty = hash "", merkleHash = hash, and merkleAppend a b = hash $ digest a <> digest b. However, a naive implementation such as that actually has some problems with what’s called a “preimage attack”. To make a long explanation short, it gives you the same digest for hashing a plain bytestring as you could get from appending two digests, and we need to be able to distinguish between the two cases (that is, force them to give different results).
We can solve this by adding salts / sigils, and differentiating between hash and merkleHash, and giving safe default implementations.
class (Hash a) => Merkle a where
merkleHash :: ByteString -> Digest a
default merkleHash :: (Hash a) => ByteString -> Digest a
merkleHash = safeMerkleHash
merkleEmpty :: Digest a
default merkleEmpty :: (Hash a) => Digest a
merkleEmpty = safeMerkleEmpty
merkleAppend :: Digest a -> Digest a -> Digest a
default merkleAppend :: (Hash a) => Digest a -> Digest a -> Digest a
merkleAppend = safeMerkleAppend
safeMerkleHash :: (Hash a) => ByteString -> Digest a
safeMerkleHash bs = hash $ concat
[ "#"
, bs
, ";"
]
safeMerkleEmpty :: (Hash a) => Digest a
safeMerkleEmpty = hash "" -- Or all zeroes, or Nothing
safeMerkleAppend :: (Hash a) => Digest a -> Digest a -> Digest a
safeMerkleAppend a b | a == safeMerkleEmpty = b
safeMerkleAppend a b | b == safeMerkleEmpty = a
safeMerkleAppend a b = hash $ concat
[ "$"
, digest a
, ":"
, digest b
, ";"
]
Note that because of the sigils, it is impossible to obtain any value from merkleEmpty or merkleAppend that you would from merkleHash, though one must take care to use merkleHash now (I should differentiate Digest and MerkleDigest to emphasize this).
So… what can we do with this unital magma hash / algebra?
Well, the first thing that comes to mind are folds, which we can use to trivially produce a merkle list or hash chain. Digests like these are often used for data integrity in things like torrents and distributed systems.
-- NOTE: Left-associative to match function application
infixl 5 <#>
(<#>) :: (Merkle a) => Digest a -> Digest a -> Digest a
(<#>) = merkleAppend
merkleFoldl :: (Merkle a, Foldable f) => f (Digest a) -> Digest a
merkleFoldl = foldl merkleAppend merkleEmpty
merkleFoldr :: (Merkle a, Foldable f) => f (Digest a) -> Digest a
merkleFoldr = foldr merkleAppend merkleEmpty
We’re just calculating the final digest here, but for real use cases we’d keep all of the hashes.
Now, on to the main thing - sparse merkle trees. Hash lists have been mostly supplanted by merkle trees, especially sparse ones, but they are just binary radix trees, also known as patricia trees. Before we implement our merkle tree, we need a few helper functions.
partitionBit :: (Bits (Digest a)) => Int -> [Digest a] -> ([Digest a],[Digest a])
partitionBit n = List.partition (not . (`testBit` n))
both :: (Bifunctor f) => (a -> b) -> f a a -> f b b
both f = bimap f f
Are you ready? Here we go! 6 lines!
merkleSetDigest :: forall a . (Merkle a) => [Digest a] -> Digest a
merkleSetDigest = go (digestSize (Proxy :: Proxy a) - 1) where
go _ [] = merkleEmpty
go _ [x] = x
go n (x:x':xs) | x == x' = go n (x:xs) -- Deduplication
go n xs = uncurry merkleAppend $ both (go (n - 1)) (partitionBit n xs)
It is trivial to obtain a sparse merkle set digest using unital magma hashing. Note that deduplication is unncessary if the inputs are already unique. If we ignore the type declaration and the deduplication, there are really only 4 lines that matter. Concise 
So what’s going on? As we traverse the list of elements, we partition them by each bit, which naturally sorts all of the digests, and as we come back up, we perform a bunch of merkleAppends to join them. Note that an empty node is the empty hash, and that appending two empty hashes results in an empty hash, and appending an empty hash to anything results in that thing. This handles all of our sparseness for us automatically, with no extra work.
Now, this just calculates the final digest, what if we wanted to actually keep the entire tree structure?
merkleSetTree :: forall a . (Merkle a) => [Digest a] -> (Digest a, [(Digest a, (Digest a, Digest a))])
merkleSetTree = go (digestSize (Proxy :: Proxy a) - 1) where
go _ [] = (merkleEmpty, [])
go _ [x] = (x, [])
go n (x:x':xs) | x == x' = go n (x:xs) -- Deduplication
go n xs = uncurry join $ both (go (n - 1)) (partitionBit n xs)
join (l,ls) (r,rs) = let top = merkleAppend l r in (top, (top, (l,r)) : (ls ++ rs))
In this version, we actually return the full merkle tree. Note the return type is effectively (TopDigest, [(ParentDigest, (LeftChildDigest, RightChildDigest))]), and that merkleSetDigest = fst . merkleSetTree. By simple convention, terminal nodes are implicit to the tree, and are not included in the list of nodes since their parent already contains them, and they themselves have no children. As a result, merkleSetTree [] = (merkleEmpty, []).
NOTE: One of the neat things about merkle sets as sets of elements is that they actually form a monoid hash, constructed from the unital magma hash. Since a merkle set is a set, we can construct a merkle set tree from elements in any order and get the same digest. This property becomes extremely useful in the future.
Now, this is pretty neat, but we can do one better. What’s better than a merkle set?
A merkle map:
partitionBitMap :: (Bits (Digest a)) => Int -> [(Digest a,b)] -> ([(Digest a,b)],[(Digest a,b)])
partitionBitMap n = List.partition (\ (k,_) -> not (testBit k n))
merkleMapDigest :: forall a . (Merkle a) => [(Digest a, Digest a)] -> Digest a
merkleMapDigest = go (digestSize (Proxy :: Proxy a) - 1) where
go _ [] = merkleEmpty
go _ [(k,v)] = merkleAppend k v
go n (x@(k,_):(k',_):xs) | k == k' = go n (x:xs) -- Deduplication on key
go n xs = uncurry merkleAppend $ both (go (n - 1)) (partitionBitMap n xs)
And a version that returns the full merkle map:
merkleMapTree :: forall a . (Merkle a) => [(Digest a, Digest a)] -> (Digest a, [(Digest a, (Digest a, Digest a))])
merkleMapTree = go (digestSize (Proxy :: Proxy a) - 1) where
go _ [] = (merkleEmpty, [])
go _ [x@(k,v)] = let h = merkleAppend k v in (h, [(h,x)])
go n (x@(k,_):(k',_):xs) | k == k' = go n (x:xs) -- Deduplication on key
go n xs = uncurry join $ both (go (n - 1)) (partitionBitMap n xs)
join (l,ls) (r,rs) = let top = merkleAppend l r in (top, (top, (l,r)) : (ls ++ rs))
Note that merkleMapDigest = fst . merkleMapTree, and that although the return type appears the same as merkleSetTree, they have slightly different conventions and handling. Note that terminal nodes are now included in the list, because their children are their key and value digest, but to find out if you’ve reached the end, you have to look for the key in the list and not find it.
That’s a bit awkward, but we’ve sacrificed heavily in the name of conciseness here. In the real world we’d probably use a a more complex but also more performant implementation. These super short implementations are here to illustrate the simplicity of the concept.
Finally, observe that merkleSetDigest [a,b,c,...] == merkleMapDigest [(a,merkleEmpty),(b,merkleEmpty),(c,merkleEmpty),...] .
import Crypto.Merkle
import Crypto.Hash.SHA3
digests = fmap (merkleHash @SHA3) [ "fee","fi","fo","fum"]
t0 = merkleSetDigest digests
(t1,_) = merkleSetTree digests
pairs = fmap (\ dg -> (dg, merkleEmpty @SHA3)) digests
t2 = merkleMapDigest pairs
(t3,_) = merkleMapTree pairs
-- All of these should return the same value
t0
t1
t2
t3
This is due to the relationship that can also be observed between the Haskell Set and Map data types, and this is not a coincidence. Producing identical digests shows that our implementation is consistent and logical, and in the future, I will be using these merkle sets and maps to build a cryptographic version of Set and Map that automatically handle proof of integrity, inclusion, exclusion, insertion, and deletion - fun! However, in order to protect against preimage attacks, I will also add salts / sigils to the merkle set and map functions, to differentiate them.
This merkle tree stuff can be found in crypto-schemes and the SHA3 from crypto-schemes-botan to test it.
That was a lot, but I’ve been building up this post for a little while, and I’m glad to finally be posting it. I’ll be writing up a much more thorough blog on this topic in the future 




 I’m glad I did because I finally got this done.
I’m glad I did because I finally got this done. )
) ), so verbatim C bindings are crucial.
), so verbatim C bindings are crucial.