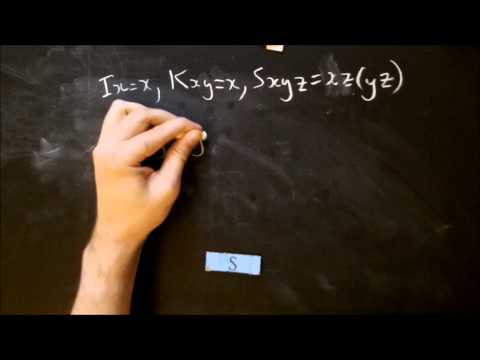I do not know whether there is a deeper connection between S and K being functionally complete and monadic structure.
If by “functionally complete”, you mean Turing-complete then yes - the Applicative instance for the partially-applied function type (->) r :
instance Applicative ((->) r) where
pure = \ a b -> a
(<*>) = \ f g x -> f x (g x)
…is Turing-complete (I think Ben Lynn also makes some comments about the Applicative-S-K connection in his presentation at Zurihac 2023). Therefore all computable functions can be defined (albeit very verbosely!) using pure and (<*>) for the Applicative reader type Reader r a = (->) r a .
Getting back on-topic - while Raymond Smullyan’s book To Mock a Mockingbird (1985), as mentioned earlier:
https://discourse.haskell.org/t/combinatory-logic/8380/14
…goes well beyond the S and K combinators, its memorable presentation of combinatory logic makes it a worthy addition to the collection of “offline” resources.