Compute Hamiltonian Cycles with List Monad

Learn
#1

I have got the code bellow and need to define the function hCycles using the list monad (and the do notation). hCycles is supposed to compute the Hamiltonian Cycles for any generic node of the graph in the image.

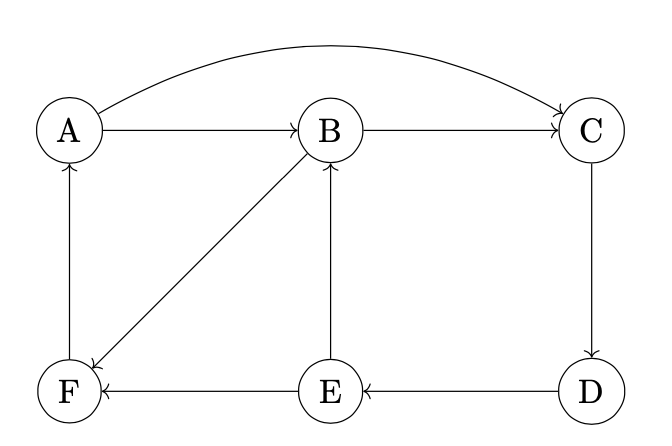
5BBHI

The thing is I’m not quite sure how to do that with the list monad and since I can’t add the starting node to the function’s arguments, how should I proceed?

-- 1. Graph structure: nodes and adjacency matrix (i.e. the edges) 
data Node = A | B | C | D | E | F deriving (Show,Eq,Ord)

adj :: (Node,Node) -> Bool
adj p = case p of
  (A,B) -> True
  (A,C) -> True  
  (A,F) -> True 
  (B,A) -> True
  (B,C) -> True
  (B,E) -> True
  (B,F) -> True
  (C,A) -> True
  (C,B) -> True
  (C,D) -> True
  (D,C) -> True
  (D,E) -> True
  (E,B) -> True
  (E,D) -> True
  (E,F) -> True
  (F,A) -> True
  (F,B) -> True
  (F,E) -> True
  (_,_) -> False

type Path = [Node]

-- 2. Auxiliary functions
adjacentNodes :: Node -> [Node] -> [Node]
adjacentNodes n ns = filter (\x -> adj(n,x)) ns

allNodes :: [Node]
allNodes = [A,B,C,D,E,F]

choice :: ([a],[a]) -> [a]
choice = uncurry (++)

-- 3. To do
hCycles :: Node -> [Path]
hCycles n = undefined

P.S.: I think I have a first version of the function:

hCycles :: Node -> [Path]
hCycles n = do 
            p <- [[n]]
            nextNode <- adjacentNodes n allNodes
            if n == nextNode
            then [p]
            else addtoEnd p allNodes

But I’m not quite sure if the if/else case is correct (since hCycles isn’t called again, I don’t even think it’s recursive, but I don’t know how to do that)…

#2

I feel

adj :: (Node,Node) -> Bool
adj p = p `elem` [(A,B), (A,C] -- add as needed

would be clearer and save space. Also do we really want adjacent nodes in a directed graph?

λ> adjacentNodes A allNodes
[B,C,F]
-- But a function that returns [B, C] (not sure about graph theory glossary)
-- would be more useful.
#4

or even:

outgoingEdges :: [(Node,[Node])]
outgoingEdges = [(A, [B,C, ...]), ...]

-- look up the adjacency list for X and check if node Y is in it
adj :: Node -> Node -> Bool
adj x y = y `elem` adjacentNodes x

-- lookup the adjacency list for node X, or return [] if not found
adjacentNodes x = fromMaybe [] $ lookup x outgoingEdges

(A Map is a similar but more efficient (and more provably correct!) way of implementing the above, but that’s out of scope here since we’re only using lists.)

You’re right @CrisTeller that your function is not recursive as written. Since you are a new learner, my recommendation is to devise an algorithm on paper, i.e. not in Haskell code, which solves the problem, and then try to translate that algorithm into code. You may find that it’s not as hard to translate as you think!

Here’s a starting point: In order for your function to build some structure up recursively, it will need to add something to an increasing list over time. What should the increasing list be, what’s the starting point for that, and what should it add at each step? [Many common recursive Haskell functions boil down to these simple questions :slight_smile: ]

Also I agree with @f-a to say that you probably don’t want (F,A) and (A,F) to both be in the adjacency list, since this imagines arrows to be going in “both directions”, whereas in the diagram that edge is definitely directed.

1 Like