Haskell classes: 25 years later

1

1998:

2023:

48 Likes
2

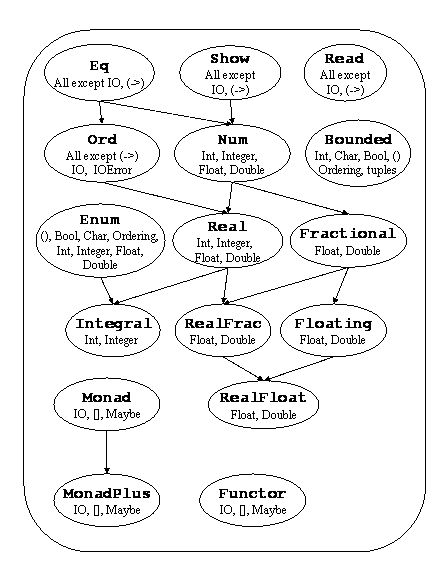
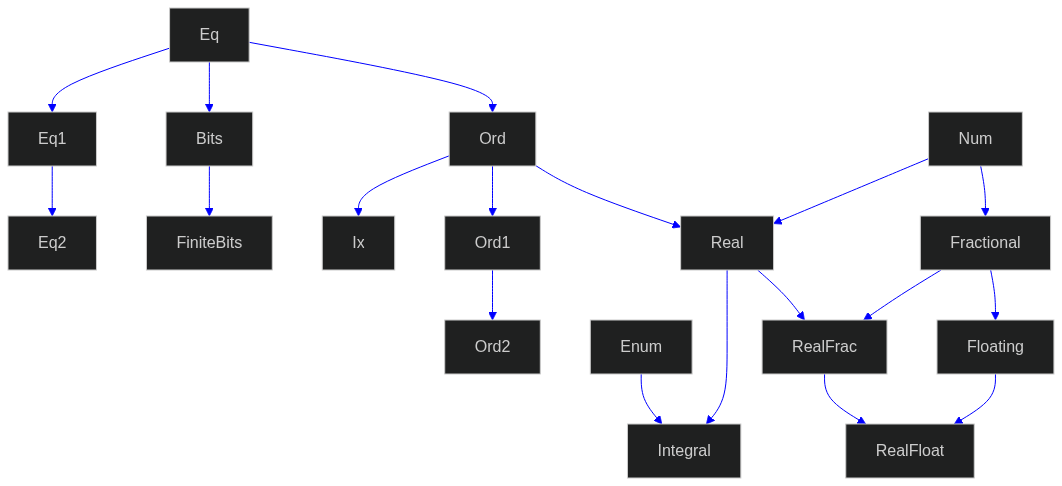
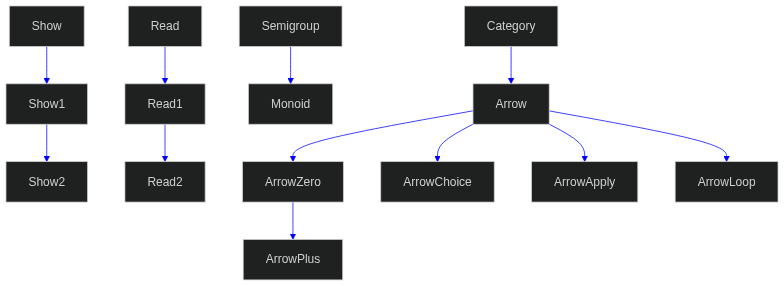
I haven’t worked out how to make the svg live on the haddocks yet, but numhask includes something like this, for its class structure, but where the boxes link to the haddocks of each class:

numhask diagram

The functionality is published in dotparse. If there’s any interest, I could do the same for these flowcharts.

3 Likes
3

Very curious that back in the day the relation between Monad and Functor did not exist. I was aware that Applicative was discovered much later, but I had never suspected that Monad and Functor used to be totally unrelated!

4

If a monad is just a monoid in the category of endofunctors, then why these classes are totally isolated from each other?

1 Like
5

Because Monad doesn’t represent all mathematical monads (just a very restricted subset) nor does Monoid represent all mathematical monoids.

3 Likes
6

Sometimes I wish Category from base is a bit more generalized:

{-# LANGUAGE TypeFamilies #-}                                                                            
import           Data.Kind (Constraint, Type)                                                            
import qualified GHC.Base  (id, (.))                                                                     
                                                                                                         
class Hask a; instance Hask (a :: Type)                                                                  
             
-- Compatible with base category by default CategoryObj to all Types                                                                                            
class Category cat where                                                                                 
    type family CategoryObj cat :: Type -> Constraint                                                    
    type instance CategoryObj cat = Hask                                                                 
    id :: CategoryObj cat a => cat a a                                                                   
    (.) :: (CategoryObj cat a, CategoryObj cat b, CategoryObj cat c) => cat b c -> cat a b -> cat a c    
                                                                                                         
class MyBizzaroObj a                                                                                     
                                                                                                         
data (:->) a b = (MyBizzaroObj a, MyBizzaroObj b) => a :-> b                                             
                                                                                                         
instance Category (:->) where                                                                            
    type instance CategoryObj (:->) = MyBizzaroObj                                                       
    id = undefined -- some bizzaro stuff                                                                 
    (.) = undefined

I vaguely recall index-core: Indexed Types is somewhat related.

1 Like
7

I would say the reason is that for you to be able to have Monad related to Monoid, via “Monoid in the Category of Endofunctors” you’d have to have a different structure to the type class hierarchy. A Categorical one, which was not the original type class hierarchy path that Haskell took.

1 Like