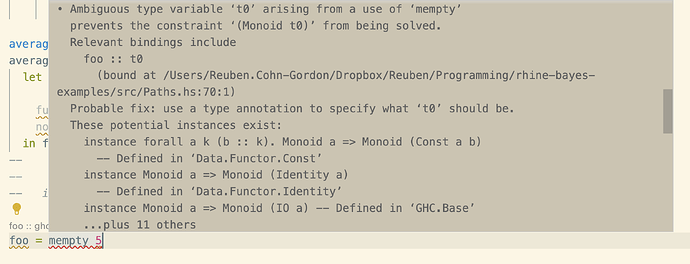
It knows because it does type inference. That is to say, whatever is on the right hand side of the equation has to have type b (because the mempty on the left has type a -> b).
Addendum :: More on () - yes I am keenly interested in that. Please expand.
Sure! So in general, a useful way to think (informally) about a type is as a set of values. For example, Bool corresponds to the set {True, False}. When we say True :: Bool, that’s like saying True is an element of the set {True, False}, or more colloquially, that True lives in the space of Boolean values.
Similarly, [Int] is the “space” of all possible lists of integers, so to say [1] :: [Int] is to say that the list [1] lives in this space.
The same holds for functions. For example, Int -> Int is the space of all functions from the space of integers to the space of integers. So the statement (\x -> x*2) :: Int -> Int is saying that the function \x -> x*2 lives in the space of integers.
Some of the common basic sets and operations on sets carry over to types in an illuminating way.
In particular, there is a set that has no values, commonly called the empty set, or the null set. This corresponds to the Haskell type Void. Void genuinely has no values in Haskell (modulo normal caveats), so there is no value a :: Void (modulo normal caveats).
There is then a set with just one value, and this corresponds to the Haskell type (). The single value that lives in the () space is also named () (Haskell often does this “pun” where values and their types share a name, which can be quite confusing if you’re not used to it). So we can write () :: ().
Things get more interesting when we turn to operations on sets. The cartesian product takes two sets a and b, and returns a x b, the set of all pairs with the left element from a and the right element from b. In Haskell, there is a corresponding notion. Given two types a and b, we have a type (a, b). For a concrete example, take the types Int and Bool. We then have a type (Int, Bool) and indeed, we have e.g. (5, True) :: (Int, Bool). In other words, (Int, Bool) is the type of pairs of an Int on the left and a Bool on the right.
Similarly for sets, there is an operation called disjoint union, which takes two sets and gives you the set containing the elements from both. In Haskell the corresponding notion, for two types a and b is Either a b. So for example, Either Int Bool contains all the elements from Int and also all the elements from Bool. For instance Right True :: Either Int Bool, and Left 5 :: Either Int Bool.
Finally, there is the set of functions from a set a to a set b. Naturally in Haskell that corresponds to the type a -> b.
OK, now for the arithmetic part. Let’s count the number of elements in various types.
size(Void) : 0
size( () ) : 1
size( (a,b) ) = size(a) * size(b)
size( Either a b ) = size( a ) + size (b).
size ( a -> b ) = size ( a) ^ size ( b )
If two types have the same size, they are isomorphic (i.e. they are basically the same, because we can map back and forth between them without losing information) so the above is often useful. For example, size(Either () a ) = 1 + size(a) = size(Maybe a), so Either () a is isomorphic to Maybe a.